1.3 Escala
Concepto de escala
Es relación entre las dimensiones de los objetos en un mapa y sus dimensiones en la realidad. La escala puede expresarse de la siguiente manera (Robinson, Sale and Morrison, 1978):
Escala numérica: Esta escala se expresa mediante una fracción que indica la relación entre una distancia en el papel y la misma distancia en el terreno. Es una fracción o razón como se muestra a continuación en donde el numerador se denomina modulo y el denominador fracción representativa:
1:10 000 o 1/10 000.
En ambos casos la escala se lee uno en diez mil y su interpretación es la siguiente:
una unidad de distancia en el mapa (Ej. 1 mm ó 1 cm) equivale a 10 000 unidades en el terreno (Ej. 10000 mm o 10 000 cm).
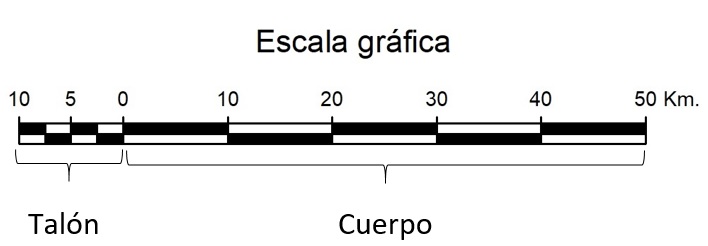
Escala gráfica lineal: Este tipo de escala es una línea dividida en segmentos numerados que permite medir la distancia en la carta sin realizar ninguna conversión. Se expresa como una línea o una barra que se ubica en la carátula explicativa del mapa. La línea se subdivide en segmentos de igual longitud para indicar la distancia en el mapa. El error máximo permisible al elaborar la escala gráfica es de 0,127 mm. La escala gráfica es útil cuando se desea reducir o ampliar un mapa ya que la relación de escala se mantiene.
La escala debe seleccionarse considerando los elementos de la realidad (puntos, líneas y polígonos) que se desean representar en el mapa.
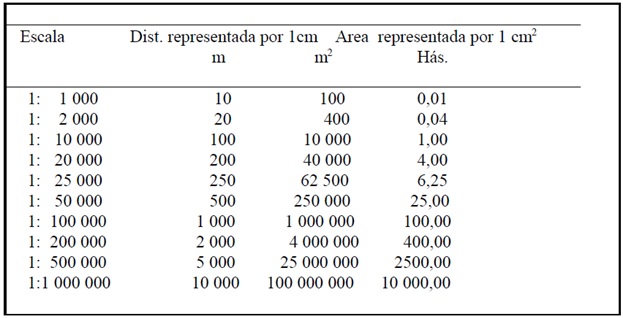
Los mapas se clasifican de acuerdo a su escala en:
- Escala grande: hasta 1: 50 000
- Escala media: 1:50 000 – 1:250 000
- Escala pequeña 1:250 000 y menores
Ahora bien, el alumno puede encontrarse frente a una serie de mapas en los cuáles no se encuentre especificada la escala de manera gráfica o numérica. En otros casos quizá se requiera obtener la distancia real que hay entre dos puntos dentro de u mapa o posiblemente, teniendo la distancia entre dos puntos conocidos por el alumno, este quiera obtener la distancia en el mapa.
Para dar respuesta a este tipo de cuestionamientos, el cálculo de la escala está regido por una expresión matemática muy sencilla conocida como Fórmula general de la escala:
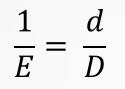
E es la escala del mapa (1,000, 50,000, etc.),
D es la distancia sobre el terreno (metros, kilómetros, millas, etc.) y
d es la distancia en el mapa (milímetros, centímetros, pulgadas, etc.)
De esta fórmula se derivan otras expresiones dependiendo del elemento que se desee conocer, por ejemplo, si se requiere conocer la escala (E) en un mapa, deberá de conocer al menos dos datos de la fórmula que resulta de despejar matemáticamente este elemento de la fórmula general, es decir, la distancia real sobre el terreno (D) y la distancia en el mapa (d).
Por otra parte, si se requiere obtener cualquiera de los otros dos elementos de la fórmula general de la escala (D o d) deberá recurrirse a realizar los despejes necesarios tal como se muestra en la siguiente imagen y después realizar los cálculos matemáticos correspondientes.

Para ejemplificar lo anterior, piense en el siguiente problema:
Se tiene un mapa histórico de la Península de Yucatán que carece de una escala gráfica o numérica, sin embargo, conocemos la distancia lineal real (D) que existe sobre el terreno entre las ciudades de Mérida y Campeche, la cual es de 150 kilómetros y también se obtuvo mediante un escalímetro que la distancia en el mapa (d) entre estos dos puntos es de 5 centímetros. A qué escala se encuentra el mapa?
Para dar respuesta a este problema, en primer lugar se debe identificar las variables o elementos con los que se cuenta (siempre deben ser al menos dos de la ecuación) y posteriormente elegir la fórmula adecuada, o bien, si la pregunta menciona explícitamente el cálculo de algún elemento de la ecuación, escoger la expresión indicada.
Como se requiere conocer la escala en el ejemplo de arriba, se utilizará la fórmula:
E = D/d
Es decir, dividir la distancia lineal real en el terreno entre la distancia en el mapa, la expresión quedaría de la siguiente manera sustituyendo los valores en la ecuación:
E = 150 Km/5 cm
Nótese que las unidades de medida son diferentes (kilómetros y centímetros) y sabemos que la escala es un elemento adimensional, es decir, no tiene unidades. Para resolver este problema, deben convertirse todas las cantidades a una u otra unidad (kilómetros a centímetros o viceversa) y después realizar las operaciones con los nuevos valores.
Si se elige convertir todas las unidades a centímetros, entonces la distancia en kilómetros deberá ser multiplicada sucesivas veces hasta encontrar las unidades requeridas, a continuación se explica este proceso muy sencillo siguiendo la lógica siguiente:
1 kilómetro tiene mil metros, por lo tanto, 150 kilómetros equivalen a 150,000 metros, es decir, para convertir kilómetros a metros, se multiplican estos por mil.
Sin embargo las unidades que se necesitan son centímetros, para lo cual se hará el siguiente razonamiento:
1 metro tiene 100 centímetros, por lo tanto 150,000 metros equivalen a multiplicar estos por cien (150,000 x 100), lo cual resulta en 15,000,000 de centímetros.
Una forma más sencilla de realizar esta operación se muestra a continuación.

Por lo tanto se puede concluir que la escala (E) del mapa histórico es de 1: 3,000,000 lo cual se lee como uno a tres millones. Pero, qué significa esta cantidad?
En otras palabras, quiere decir que una unidad de medida en el mapa (1 centímetro, milímetro, decímetro, etc.) equivale a tres millones de esas unidades en el terreno.
Por ejemplo, si ahora ya sabemos cuál es la escala (1: 3,000,000) y medimos 1.2 centímetros en el mapa, esto equivale a multiplicar esa cantidad por tres millones, lo cual resulta en 3,600,000 centímetros, que equivale a 36 kilómetros.