1.5 Proyecciones cartográficas
Las proyecciones cartográficas.
En la disciplina cartográfica, no es posible representar una superficie esférica sobre un plano sin modificar las propiedades geométricas de los elementos de esta, por esta razón, a lo largo de la historia los cartógrafos han desarrollado diversas transformaciones matemáticas para lograr este objetivo, a estas transformaciones se les denomina proyecciones cartográficas.
Proyectar significa representar una parte o la totalidad de la superficie terrestre sobre una superficie plana y, dado que la superficie terrestre tiene la forma de un geoide, no hay forma de representar en plano la tridimensionalidad sin evitar la deformación, es por ello que algunas proyecciones modernas - a partir de modelos matemáticos -, han tratado de resolver “la cuadratura del círculo”.
Un esferoide no se puede aplanar para dejarlo en dos dimensiones: lo mismo que una piel de naranja, se romperá inevitablemente. La representación de la superficie de la Tierra en dos dimensiones provoca la distorsión de la forma, el área, la distancia o la dirección de los datos. Una proyección cartográfica utiliza fórmulas matemáticas para relacionar las coordenadas esféricas del globo con coordenadas planas, planares.

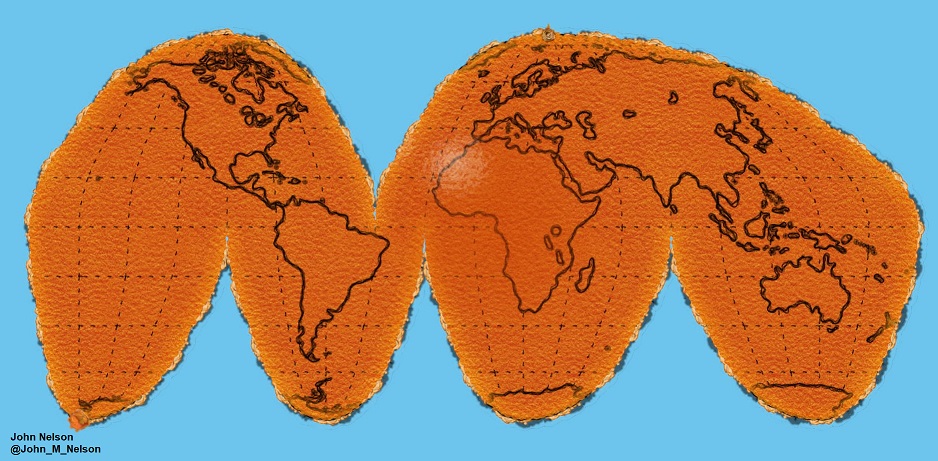
Ahora bien, para transformar esta superficie esférica, se necesita tener una figura geométrica desarrollable en donde hacerlo, para este fin se utiliza el cono, el cilindro y el plano (como si se tratara de una hoja de papel).
Estas formas geométricas auxiliares, en combinación con la posición en la que se coloquen (normal, paralela o inclinada al ecuador), así como la situación del punto de vista dan lugar a todas las proyecciones cartográficas que existen actualmente.
Las proyecciones producen distintos tipos de distorsiones. Algunas proyecciones están diseñadas para minimizar la distorsión de una o dos de las características de los datos. Una proyección podría mantener el área de una entidad pero modificar su forma. En el gráfico siguiente, los datos cercanos a los polos se extienden.
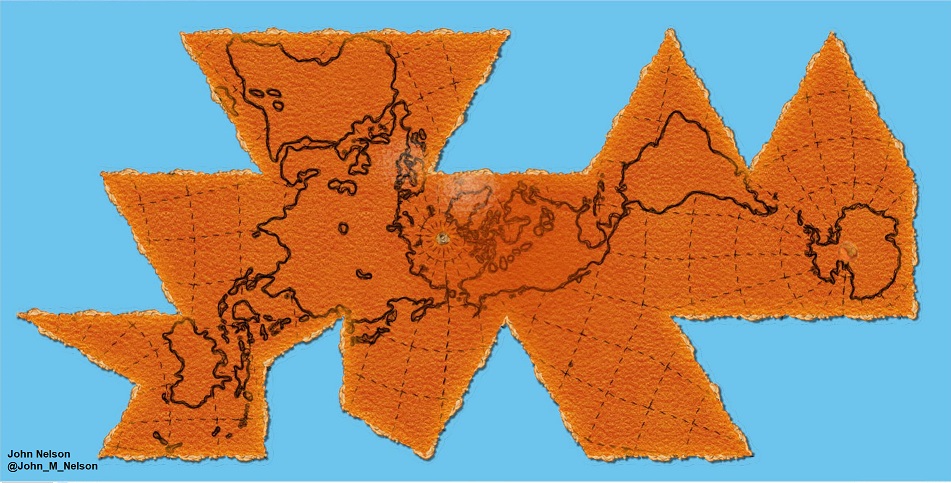
Las proyecciones cartográficas están diseñadas para fines específicos. Una proyección cartográfica podría utilizarse para datos a gran escala de un área limitada, mientras otra se utiliza para un mapa del mundo a pequeña escala.
De acuerdo con las propiedades de forma, área, distancia y dirección, se han inventado proyecciones conformes, equivalentes, equidistantes y azimutales.
Proyecciones conformes
Las proyecciones conformes conservan la forma local. Para conservar cada uno de los ángulos que describe las relaciones espaciales, una proyección conforme debe mostrar las líneas perpendiculares de la cuadrícula con intersecciones en ángulos de 90 grados en el mapa. Para que una proyección cartográfica consiga hacer esto, debe mantener todos los ángulos. La desventaja es que el área delimitada por una serie de arcos puede distorsionarse mucho en el proceso. Ninguna proyección cartográfica puede conservar las formas de áreas mayores.
Proyecciones equivalentes
Las proyecciones equivalentes conservan el área de las entidades mostradas. Para ello, se distorsionan las demás propiedades: forma, ángulo y escala. En las proyecciones equivalentes, es posible que los meridianos y los paralelos no se intersequen en ángulos rectos. En algunas ocasiones, sobre todo en mapas de áreas pequeñas, la distorsión de las formas no es obvia y resulta difícil distinguir una proyección de áreas equivalentes de una proyección conforme, a menos que se haya documentado o medido.
Proyecciones equidistantes
Los mapas equidistantes conservan las distancias entre ciertos puntos. Ninguna proyección mantiene correctamente la escala en un mapa completo. Sin embargo, en la mayoría de los casos hay una o varias líneas en el mapa a lo largo de las cuales la escala se mantiene correctamente. La mayoría de las proyecciones equidistantes tienen una o varias líneas en las que la longitud de la línea en un mapa tiene la misma longitud (a la escala del mapa) que la misma línea en el globo, sin tener en cuenta si se trata de un círculo grande o pequeño, o si es una línea recta o curva. Se dice que tales distancias son reales. Por ejemplo, en la proyección sinusoidal, las longitudes del ecuador y de todos los paralelos son reales. En otras proyecciones equidistantes, el ecuador y todos los meridianos son reales. Otras proyecciones (por ejemplo, la equidistante de dos puntos) muestran la escala real entre uno o dos puntos y cada uno de los demás puntos del mapa. Tenga presente que ninguna proyección es equidistante con origen y destino en todos los puntos de un mapa.
Proyecciones de dirección real
La ruta más corta entre dos puntos de una superficie curvada tal como la Tierra es a lo largo del equivalente esférico de una línea recta en una superficie plana. Se trata del círculo grande en el que descansan los dos puntos. Las proyecciones de dirección real o acimutales mantienen algunos de los arcos del círculo grande, y ofrecen correctamente las direcciones o acimutes de todos los puntos del mapa respecto al centro. Algunas proyecciones de dirección real son también conformes, equivalentes o equidistantes
Tipos de proyección
Dado que los mapas son planos, algunas de las proyecciones más sencillas se convierten en formas geométricas que se pueden aplanar sin extender sus superficies. Dichas superficies se denominan superficies desarrollables. Ejemplos comunes son los conos, cilindros y planos. Una proyección cartográfica proyecta de manera sistemática ubicaciones situadas en la superficie de un esferoide sobre posiciones representativas situadas sobre una superficie plana, utilizando para ello algoritmos matemáticos.
El primer paso que debe darse para proyectar desde una superficie a otra es ubicar uno o más puntos de contacto. Cada contacto es un punto (o línea) de tangencia. Una proyección planar es tangencial al globo en un punto determinado. Los conos y cilindros tangenciales tocan el globo a lo largo de una línea. Si la superficie de la proyección interseca el globo en lugar de tocar sin más su superficie, la proyección resultante es una secante en lugar de una tangente. Sea el contacto tangente o secante, los puntos o líneas de contacto son importantes porque definen ubicaciones de distorsión cero. Entre las líneas de escala real se encuentran los paralelos estándar y el meridiano central, que en ocasiones se denominan líneas estándar. En general, la distorsión es directamente proporcional a la distancia con el punto de contacto.
Muchas de las proyecciones cartográficas más comunes se clasifican según la superficie de la proyección utilizada: cónica, cilíndrica o planar.
A continuación, se muestran los tipos de proyección más habituales: cónica, cilíndrica y planar.
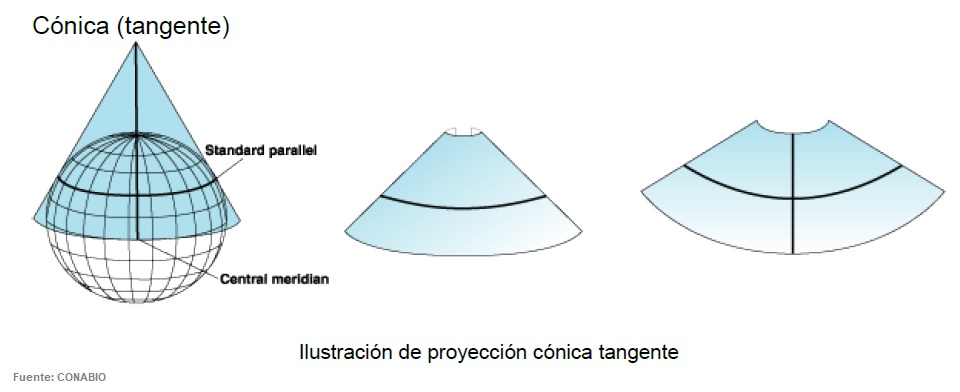
Se sitúa un cono imaginario sobre el globo. El cono y el globo se tocan a lo largo de una línea de latitud. Dicha línea es el paralelo estándar. El cono se corta a lo largo de la línea de longitud opuesta al meridiano central y se convierte en un plano.
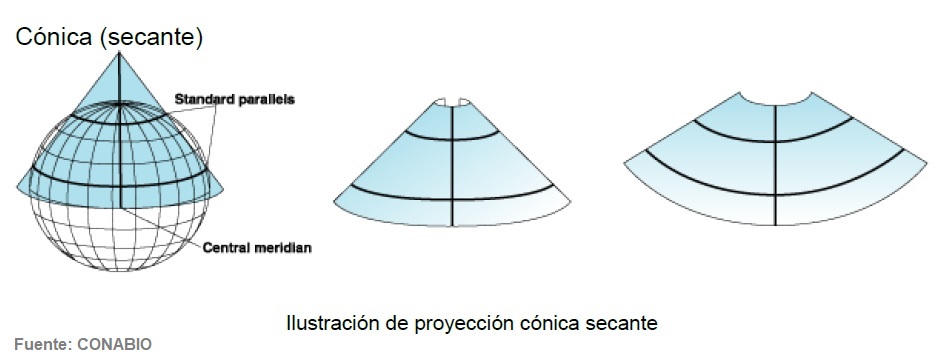
Se sitúa un cono imaginario sobre el globo que atraviesa parte de la superficie de éste. El cono y el globo se tocan a lo largo de dos líneas de latitud. Dichas líneas son los paralelos estándar. El cono se corta a lo largo de la línea de longitud opuesta al meridiano central y se convierte en un plano.
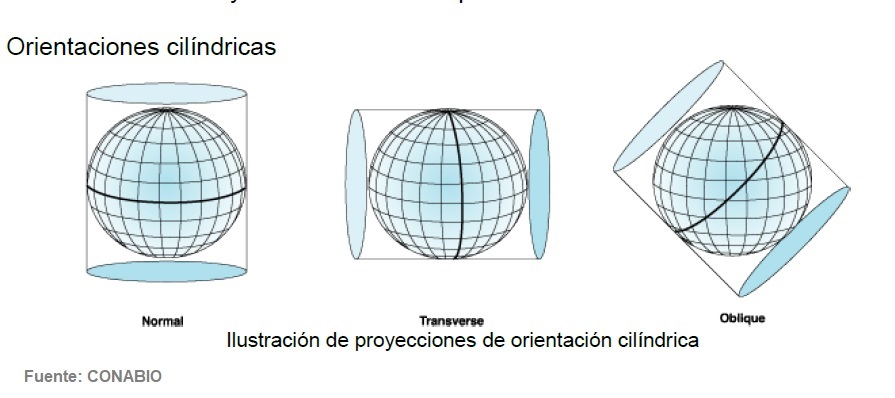
Se sitúa un cilindro imaginario alrededor del globo. El cilindro puede tocar el globo a lo largo de una línea de latitud (tipo normal), a lo largo de una línea de longitud (tipo transversal) o a lo largo de otra línea cualquiera (tipo oblicuo).

Se sitúa un plano imaginario sobre el globo. El plano puede tocar el globo en uno de sus polos (tipo polar), en el ecuador (tipo ecuatorial) o en otra línea cualquiera (tipo oblicuo).
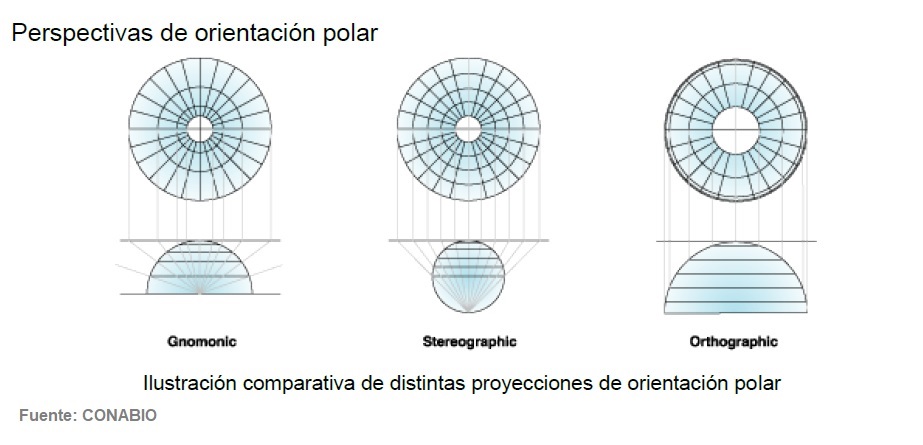
Las proyecciones planares o acimutales pueden reproducirse con diferentes perspectivas. El punto de proyección gnomónica se sitúa en el centro del globo. En la proyección estereográfica, el punto de contacto se sitúa en el polo opuesto del globo. El punto de perspectiva en la proyección ortográfica está situado en el infinito.
La proyección UTM (Proyección Universal Transversa de Mercator)
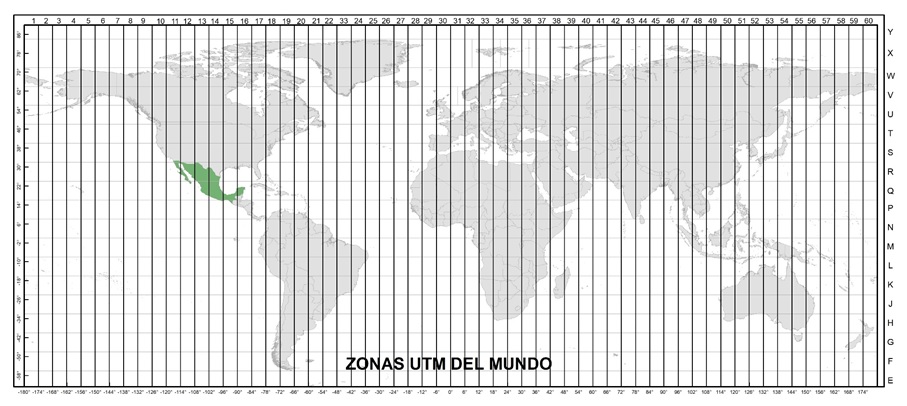
Cada zona tiene un ancho de seis grados de longitud, tres grados en cada dirección desde el meridiano tangente. Las zonas del sistema se numeran en secuencia de oeste a este comenzando con 1 para la zona que cubre los 180º. Además, las zonas se subdividen en filas, con una altura de 8º, a las que se les asignan letras de sur a norte comenzando a los 80º sur con la letra C. Como la distorsión en los polos es muy grande, no se definen zonas para las regiones que se encuentran más allá de estos límites.
Cada zona tiene un ancho de seis grados de longitud, tres grados en cada dirección desde el meridiano tangente. Las zonas del sistema se numeran en secuencia de oeste a este comenzando con 1 para la zona que cubre los 180º. Además, las zonas se subdividen en filas, con una altura de 8º, a las que se les asignan letras de sur a norte comenzando a los 80º sur con la letra C. Los meridianos centrales son: 87°, 93°, 99°,105°, 111° y 117°. Y le corresponden las zonas UTM de la 11 a la 16.
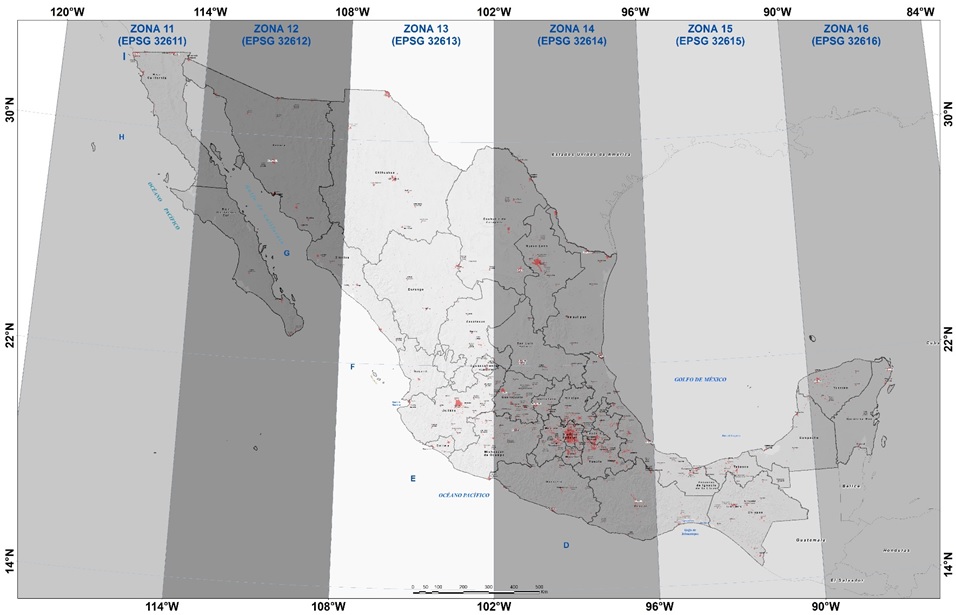
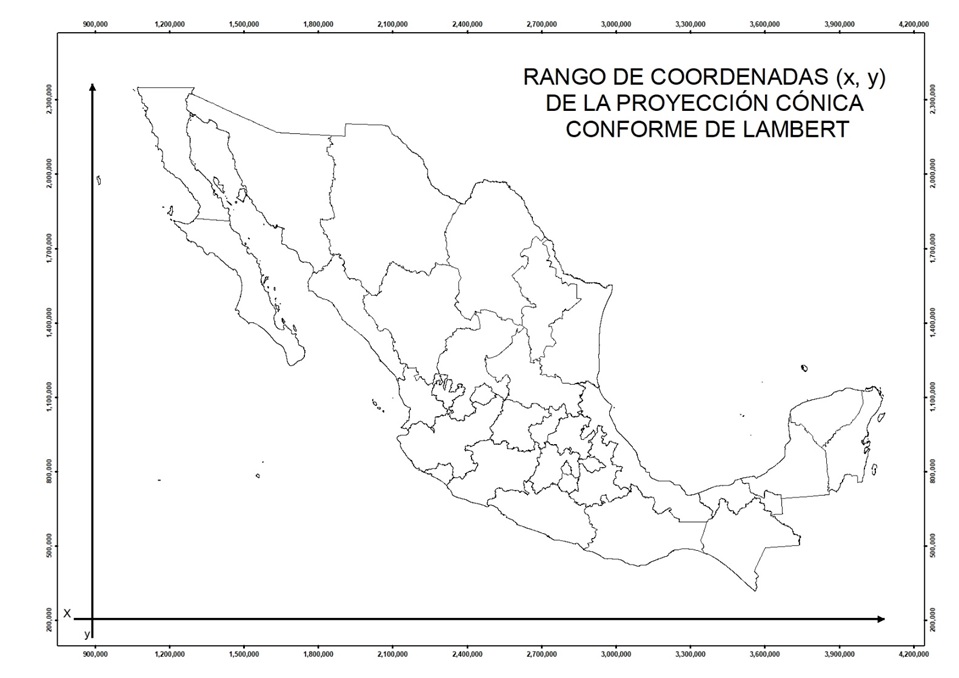
Las proyecciones utilizadas en el INEGI son la UTM para escalas hasta 1:500,000, la proyección Cónica Conforme de Lambert con dos paralelos base a 17º 30' y 29° 30' , y la Proyección de Mercator simple para la cartografía oceanográfica.